GPU 后端优化（一）

为什么会有GPU后端优化博客？在阅读BladeDISC以及IREE等源码的过程中，发现当逐步接触后端代码生成/运行时系统调度时，由于本人没有深入接触过GPU体系架构（基础太差），很多优化pass难以理解。这一过程使我认识到对于底层系统架构的深入理解往往比具体的编译技术，编译框架（MLIR/LLVM）而言更为重要。本系列主要记录我补习GPU架构知识的学习历程（开个坑，主要用于激励我自学CUDA，不然太摆了）。目前初步的计划，该系列会有如下几篇博客：

GPU后端优化（一）：主要包括GPU后端优化基础知识

GPU后端优化（二）：机器学习编译实战部分，以MLIR做GPU代码生成论文为概览，结合IREE和BladeDISC开源代码分析

GPU后端优化（三）：结合CUDA算子优化博客，学习CUDA算子开发过程和对应算子编译手段

GPU后端优化（四）：高阶GPU体系结构，结合GPU架构书籍进行解读

GPU后端优化基础知识

在日常学习中，由于我的工作和编译器关联度较大，因此一般都是在阅读开源项目的pass源码。这其中如果涉及GPU相关的优化pass，遇到不懂的可能直接询问chatgpt或是一些博客寻找答案。久而久之发现自己虽然好像能够读懂编译器的后端生成pass，但往深处探讨，为什么这些pass是这样的顺序，为什么GPU需要这些pass，很多问题其实都回答不上来。归根结底，是对于GPU优化的原理知识以及优化之间的关联细节没有真正去仔细思考和学习。

印度理工的学者的一篇利用MLIR搭建高性能GPU算子自动生成的文章，是我们开始的很好的起点。这篇文章完全基于MLIR基础设施，并做少量修改，同时是一个完整的GPU优化生成流程，是十分值得学习的。本章节的目的就是尽量扫盲，使一些原本不那么清晰或是没涉及过的优化概念尽量明晰，为读懂该文章做好准备工作。

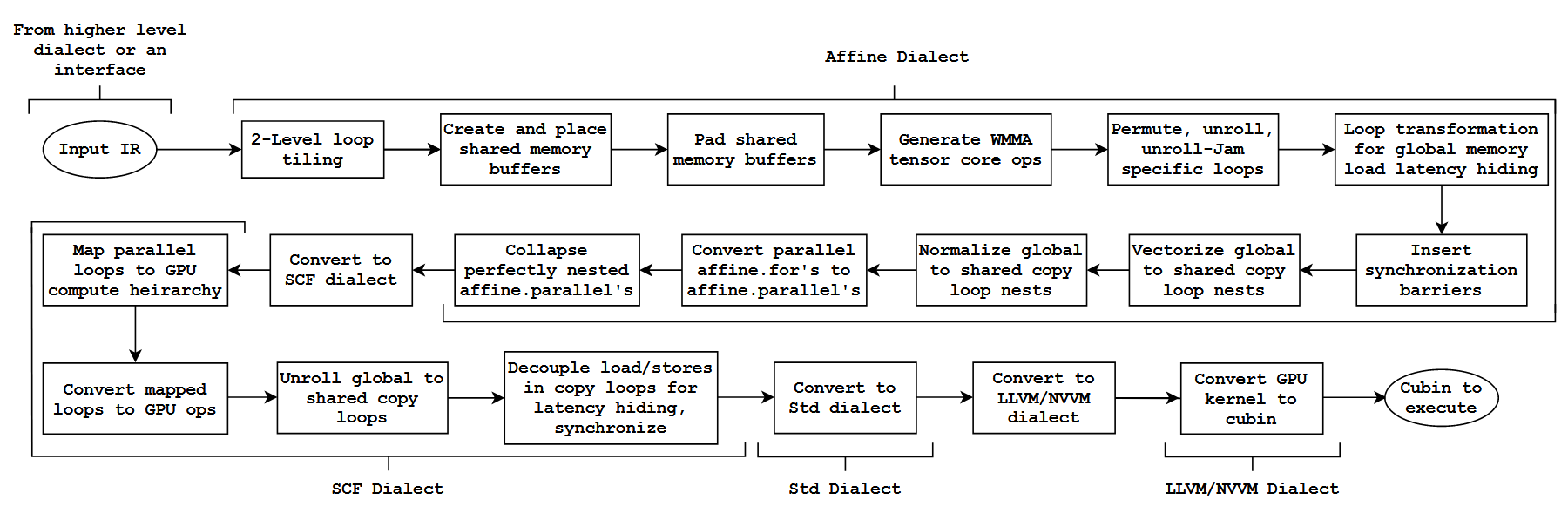
如上图所示是论文中的GPU算子生成流水线，也是我们补足GPU后端编译优化基础知识的概览。后续内容按照流水线展开，大体内容划分如下：

Loop Tiling优化
存储优化（共享内存开辟，padding，coalesce内存）
tensor core适配（WMMA api）
global memory latency hiding
GPU流水线技术
一些杂项

同时本章节还会补充如何计算优化的瓶颈：（计算瓶颈和访存瓶颈）

Loop Tiling优化

这一章节主要参考一篇文章了解 Loop Tiling 优化，这篇博客讲解非常到位，强烈建议有兴趣的读者仔细阅读。本篇文章的解读顺序和原博客不太一致，选择先列出tiling算法步骤，然后以一个具体例子带着大家走一遍算法步骤，解读每一步原理。

Tiling算法步骤

算法：

设总共有 N 层循环，从外向内分别是 0,1,...,N-1

从内向外，逐步分析 N-2,N-3,...,0（先排除掉最内层循环）

对于每层循环 L ，看其 idx=0,1,... 时，是否有 array 可能被反复读取。

若有，则 tile 第 L+1 层循环。

都做完之后，再分析 基于新循环是否仍然有可 tile 的部分

上述算法初看比较抽象，选择通过一个矩阵乘法例子来走一遍该规则，以简化算法理解。

首先我们要tiling的计算任务是NxNxN的矩阵乘（现实场景由于矩阵的维度，cache的维度有很多dirty work和边界trick，这里默认矩阵是“完美的”）。伪代码如下图所示：

for i in range(0, N):            # i,k,j，访问符合行优先原则
  for k in range(0, N): 
    for j in range(0, N):
      C[i][j] += A[i][k] * B[k][j]

根据算法描述，首先分析k维度遍历过程中是否有array反复读取（k维度对应N-2维度）。发现c[i][j]的遍历和k维度无关，因此可以tile j这个维度，得到如下伪代码：

for j_o in range(0, N, T_j):                           # j_i 对应j维度的外层维度，从0到N，步长为T
    for i in range(0, N):
        for k in range(0, N):
            for j_i in range(j_o, j_o+T_j):            # j_o 对应j维度的内层循环
                c[i][j_i] += A[i][k] * B[k][j_i]

分析tiling后伪代码，通过选取合适的T（适配L1缓存大小），则c[i][j_i]可以做到在k迭代过程中一直缓存在cache中。继续我们的tiling算法，该尝试k的上一层维度，i维度。发现B[k][j_i]在遍历过程中和i的值无关，因此可以对下一层，即k做优化，使得B[k][j_i]适配缓存。如下是伪代码：

for k_o in range(0, N, T_k):
  for j_o in range(0, N, T_j):
    for i in range(0, N):
      for k_i in range(k_o, k_o+T_k):
        for j_i in range(j_o, j_o+T_j):
          C[i][j_i] += A[i][k_i] * B[k_i][j_i]
# 这样，k_i=0,1... 时，C[i_i][j] 始终在 cache 中；i=0,1.. 时，B[k_i][j_i] 也始终在 cache 中

至此，走完算法的第一部分流程，来到第二部分：需要分析 基于新循环是否仍然有可 tile 的部分。这部分的逻辑是，对于k维度和j维度做的tiling分块，对于最顶层（初始的顶层）i维度产生影响，目前i维度已不是顶层维度。i维度之上的j_o遍历过程中，下一层i的遍历跨度是N，比较大，是难以存入cache中的，因此需要对i也做tiling优化。伪代码如下：

# 又因为循环 i 从最外层循环变成了内循环，对于其上层循环 j_o 来说，当 j_o=0,1,...时，A[i][k_i] 是被反复读取的，因此也可以 tile 循环 i
for i_o in range(0, N, T_i):
  for k_o in range(0, N, T_k):
    for j_o in range(0, N, T_j):
      for i_i in range(i_o, i_o + T_i):
        for k_i in range(k_o, k_o + T_k):
          for j_i in range(j_o, j_o + T_j):
            C[i_i][j_i] += A[i_i][k_i] * B[k_i][j_i]
# 注意，内三层循环仍然是按照 i_i,k_i,j_i 的顺序，因此仍然满足 RowMajor 的顺序读取

至此，完成L1的tiling优化。可以看到，目前我的变换出的代码，在i_i，k_i和j_i维度都已经是tiling分块的。

结束了？Too Naive！！！:fire:

现代体系结构（从CPU到GPU到ASIC），均有多层级缓存体系。让我们继续研究一下代码，思考一下如果有L2 cache，该如何继续tiling？目前的矩阵乘运算已经适配L1缓存，可以看到j_o维度的循环，已经是完美缓存的。但是对于k_o循环而言，下一层j_o循环则成了严重的性能瓶颈。j_o循环总步长为N，这之间又是大量的cache miss。这一部分就需要L2缓存来加速存储交互了。继续我们的算法，以k_o维度为新的起点由内向外，分块的大小按照L2缓存来，继续一轮迭代，最终的结果：

for j_oo in range(0, N, T2_j):
  for i_o in range(0, N, T_i):
    for k_o in range(0, N, T_k):
      for j_oi in range(j_oo, j_oo + T2_j, T_j):
        for i_i in range(0, N, T_i):
          for k_i in range(k_o, k_o + T_k):
            for j_i in range(j_oi, j_oi + T_j):
              C[i_i][j_i] += A[i_i][k_i] * B[k_i][j_i]
# 这样的话，内三层循环 i_i, k_i, j_i （对应的 Tile size 为 T_i, T_j, T_k）放到 L1 Cache 里。
# 外层循环 j_oi （对应Tile size 为 T2_j） 就可以放到更大的 L2 Cache 里。于是便在 L2 里形成了对 C[i_i][j_i] 的复用

同理，可以继续向上，做k_o和i_o的分块，不再详细阐述了。

存储优化

Shared Memory

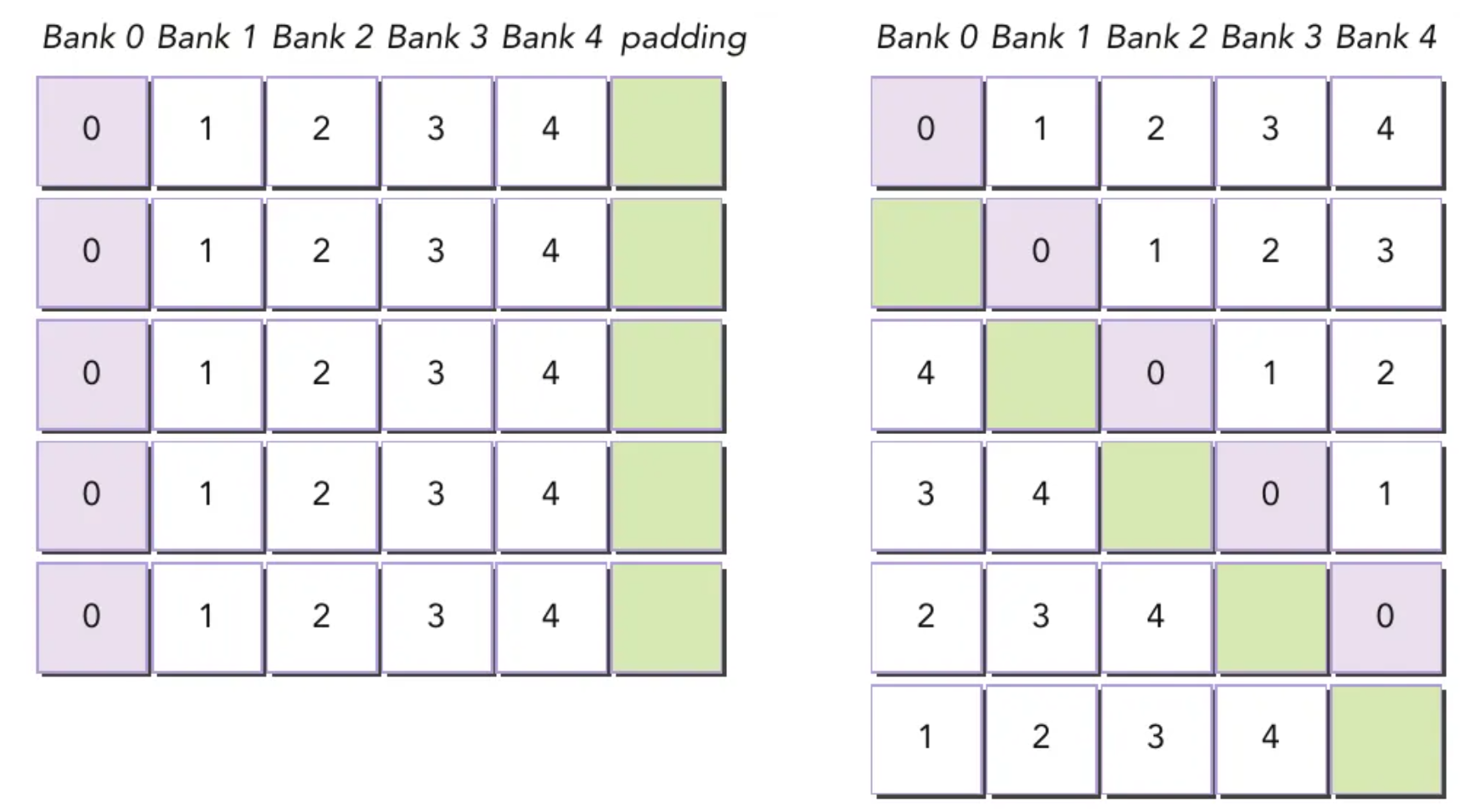
为什么要Padding？

这部分文章重点参考GPU shared memory解读博客，Bank Conflict优化博客和Padding优化bank conflict原理。理解为什么GPU管线需要做padding，首先需要补充一下Bank Conflict相关的知识。

参考CUDA shared memory资料。

Shared memory has 32 banks that are organized such that successive 32-bit words map to successive banks. Each bank has a bandwidth of 32 bits per clock cycle.

A shared memory request for a warp does not generate a bank conflict between two threads that access any address within the same 32-bit word (even though the two addresses fall in the same bank). In that case, for read accesses, the word is broadcast to the requesting threads and for write accesses, each address is written by only one of the threads (which thread performs the write is undefined).

To achieve high memory bandwidth for concurrent accesses, shared memory is divided into equally sized memory modules (banks) that can be accessed simultaneously. Therefore, any memory load or store of n addresses that spans b distinct memory banks can be serviced simultaneously, yielding an effective bandwidth that is b times as high as the bandwidth of a single bank.
— 《Using Shared Memory in CUDA C/C++》

However, if multiple threads’ requested addresses map to the same memory bank, the accesses are serialized. The hardware splits a conflicting memory request into as many separate conflict-free requests as necessary, decreasing the effective bandwidth by a factor equal to the number of colliding memory requests. An exception is the case where all threads in a warp address the same shared memory address, resulting in a broadcast. Devices of compute capability 2.0 and higher have the additional ability to multicast shared memory accesses, meaning that multiple accesses to the same location by any number of threads within a warp are served simultaneously.
— 《Using Shared Memory in CUDA C/C++》

上述资料可以总结为如下要点：

无bank conflict情况：

warp 内所有线程访问不同 banks，没有冲突；

warp 内所有线程读取同一地址，触发广播机制，没有冲突。

存在bank conflict情况：

warp 内多个线程访问同一个 bank，且地址不同

padding优化如下图所示：

Memory Coalesce

这个计算的讲解主要参考SGEMM_CUDA博客。我们先补充GPU技术基础知识，然后逐步引入memory coalesce的概念

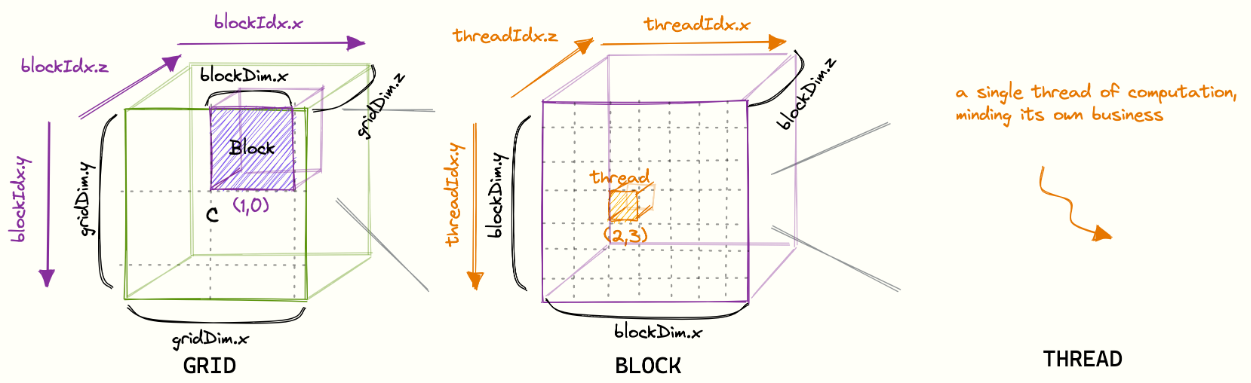
GPU的最小调度执行单元是Warp，Warp的线程数统一是32
GPU的每个SM（threadBlock给到SM执行）有4个Warp Scheduler，通过调度warp的执行，达到掩藏延迟的目的
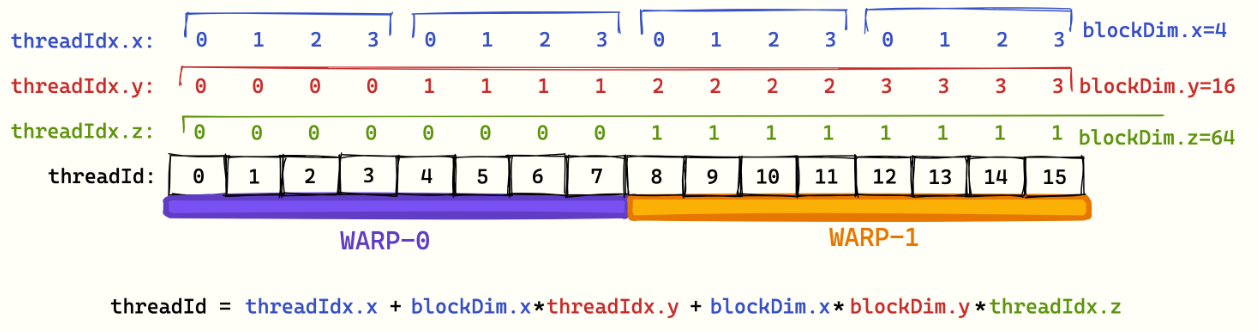
如何决定哪些线程组合在一起运行？通过threadId的计算决定，相邻threadId会被分配到同一warp中执行。具体计算公式如下：
1
threadId = threadIdx.x+blockDim.x*(threadIdx.y+blockDim.y*threadIdx.z)
这里有个十分反直觉的点：threadId的计算是列主序，即y和z一样，x相邻，threadId相邻。如下图所示是一个threadId和warp组合的示意图，其中为了简化表示，下图是8个threads一个warp：
有了之前三个铺垫，我们开始引入memory coalesce知识：同一warp的thread，对于存储空间的顺序访问（物理空间连续），可以合并成一此访问执行（类似transaction概念）。如下图所示，4个连续的物理存储访问可以合并成一次load操作，很好地体现了memory coalesce的作用。

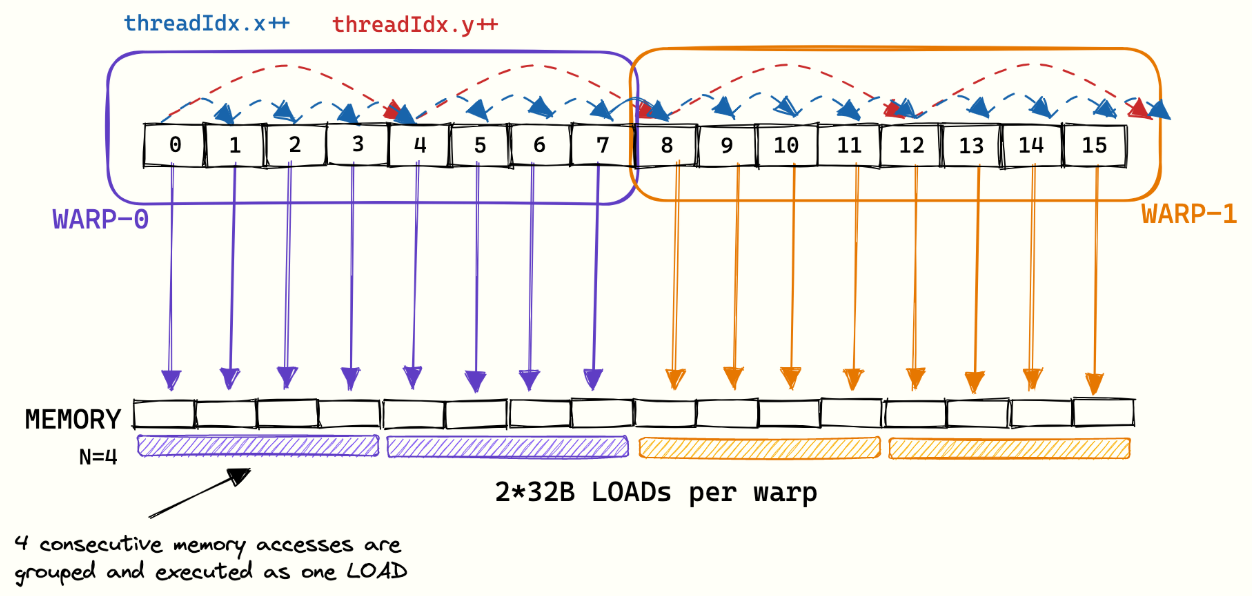
上述4点很好的阐述清楚了memory coalesce的原理，我们接下来了解一些GPU的参数：

GPU支持32B，64B，128B的存储访问。也就是说，一个warp是32个threads，如果每个thread访问连续的fp32的数据，则是32*4B=128B，正好使用128B的存储访问指令即可。

至此有关memory coalesce的相关知识已补充介绍完毕。

GPU流水线技术

计算瓶颈，访问瓶颈估算

在讲解完上述诸多GPU优化技术后，在现实实践中，我们需要能够先根据计算任务和GPU性能估算出理论的计算访问峰值，判断目前的主要瓶颈，然后再应用诸多优化手段进一步压榨性能。这一部分讲解参考sgemm博客对于A6000架构的性能估算，主要分为如下几个步骤：

首先我们先分析我们的计算任务：对于一个4092x4092矩阵FMA运算（乘加运算），需要计算总的计算FLOPS和存储访问量：
- 总FLOPS：2 * 4092^3 + 4092^2（FMA是两个FLOP）
- 总数据读取：3 * 4092^2 * 4B（是F32，为4bytes）
- 总数据存储：4092^2 * 4B
由此估算出最小总存储量是268MB
结合NVIDIA给的参数，A6000在fp32上的计算能力为30TFLOPs/s，存储带宽为768GB/s。
完成一次计算需要4.5ms，而完成一次数据传输0.34ms
由此得出理论峰值处，应该是计算瓶颈。但目前测试依旧处于存储瓶颈，可以借助于下图的roofline模型加以理解。

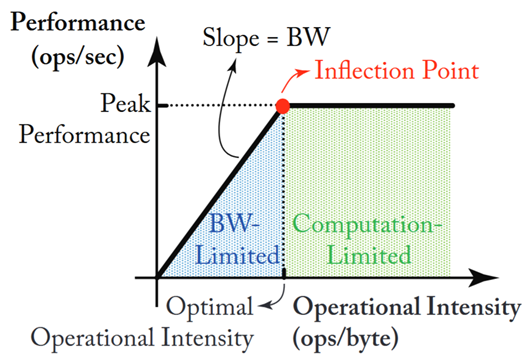
除去上述计算方式，还有Arithmetic Intensity(FLOPs/bytes)这一概念用于判断瓶颈。如果该值很高，则是计算瓶颈，否则是访问瓶颈。

Occupancy分析

GEMM cuda blog对于Occupancy的解释如下：Occupancy is defined as the ratio between the number of active warps per SM and the maximum possible number of active warps per SM.即一个SM可以同时支持很多个block，每个block可以由多个warp执行。但是受限于资源约束，真正可执行的warp是有限的，occupancy衡量的就是如何最大化可执行warp数。资源约束可以分为三个方面：（1）寄存器数量（2）共享内存大小（3）线程数量

在该博客中，对于occupancy也有详细的计算，感兴趣读者可以自行参考分析。对于occupancy的详细计算，可以参考Occupancy计算博客，实际工作中对于occupancy的计算，可以参考CUDA Occupancy计算器。

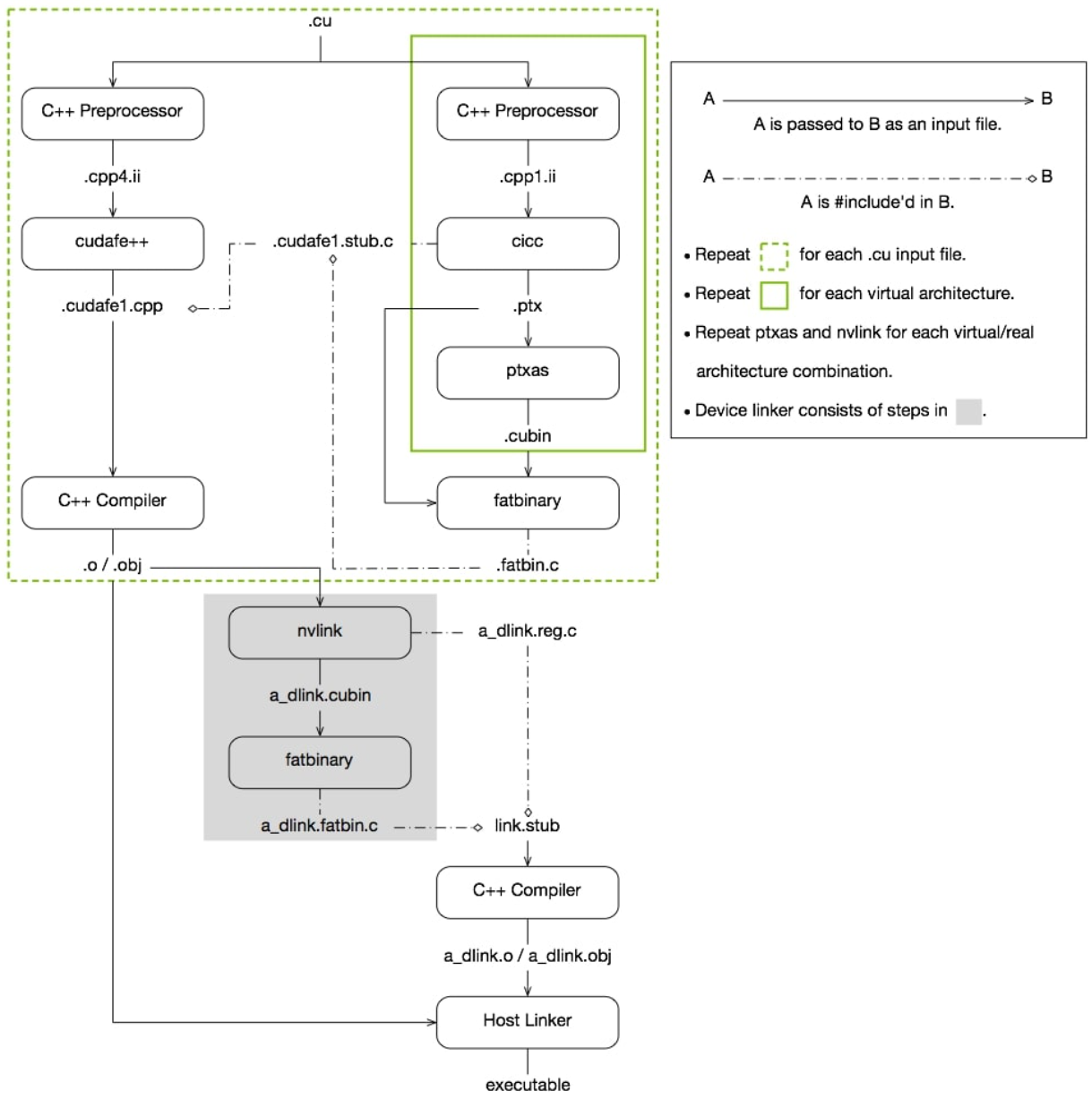
CUDA编译流程

前面几小节按照MLIR优化GEMM算子论文中的管线（pipeline），补充了面向GPU的相应优化技术点。这一小节则讲解在cuda中是如何做代码生成，讲解一个大概的流程框架。这个流程可以分为两部分来讲解，一是最常用的英伟达闭源工具nvcc编译器的编译流程，二是基于MLIR基础设施的编译流程，从mlir系统接入LLVM IR，然后借助于LLVM成熟编译器进行编译生成。

Leon's Blog